استنتاج المسقط الثالث لجسم ما بمعرفة مسقطين له:

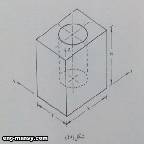
من المعلوم أن أي مجسم فراغي يمكن وصفه بثلاثة أبعاد إذا اعتمدنا المحاور الكارتيزية الثلاثة X, Y, Z. أما في مسقط أي جسم على مستوى ما فيمكن توضيح بعدين فقط حسب وضع المستوى من الجسم فمثلاً يمكن توضيح البعدين X, Y إذا نظرنا للجسم الموضح بالشكل 45 في اتجاه متعامد على المستوى الأفقي XY أي أن المسقط الأفقي للجسم يظهر البعدين X, Y لهذا الجسم وبالمثل فإن البعدين X, Z يظهران في المسقط الرأسي للجسم.
ومعنى ذلك أن وجود مسقطين للمجسم يكون كافياً لمعرفة كل أبعاد المجسم وبالتالي يمكن تخيل شكله الحقيقي بجميع أبعاده. وبالتالي فإنه من الممكن بعد التخيل للمجسم استنتاج المسقط الثالث له حيث أن أبعاده Y, Z قد تم تعريفها في المسقطين الآخرين.
يوضح الشكل (46) مثالاً لاستنتاج المسقط الجانبي للجسم بمعلومية المسقطين الرأسي والأفقي وفيه يحدد البعد الرأسي للمسقط الجانبي Z من المسقط الرأسي بواسطة مستقيمين أفقيين كما في الشكل ويحدد البعد الأفقي Y بإدارة البعد نفسه مأخوذاً من المسقط الأفقي ونلاحظ أنه لمعرفة شكل أي جزء فإنه يجب دراسة المسقطين المعطيين لهذا الجزء في نفس الوقت فالدائرة الموجودة بالمسقط الأفقي ذات القطر (a) يمكن أن يكون ثقباً في المجسم كما في الشكل أو اسطوانة أعلاه.
وبنفس الطريقة السابقة يمكن استنتاج المسقط الأفقي بمعرفة المسقطين الرأسي والجانبي.