ثانياً: الإسقاط المتوازي (Parallel Projection)

إذا تخيلنا أن مركز الإبصار قد ابتعد إلى ما لا نهاية فإن خطوط الإسقاط الصادرة منه تصبح متوازية، ويسمى نوع الإسقاط عندئذ بالإسقاط المتوازي وفيما يلي استعراض لأهم أنواعه وأكثرها استخداماً.

1- الإسقاط الأيزومتري Isometric Projection:

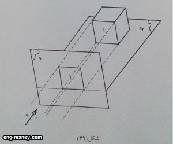
إذا تصورنا على سبيل المثال مكعب يرتكز بقاعدته على المستوى M عامودي على مستوى الإسقاط S بحيث يكون الوجه I موازياً لمستوى الإسقاط وكانت خطوط الإسقاط متوازية في اتجاه R وعامودية على المستوى ٍS فإن مسقط المكعب في المستوى ٍS هو مربع.

وإذا أدير هذا المكعب حول محوره الرأسي بزاوية أقل من 90° (45° مثلاً) فإن صورة المكعب في المستوى S تكون ممثلة لمسقط الوجهين II, I.

وعند إمالة المكعب وهو في هذا الوضع إلى الأمام بحيث يكون قطره ef عمودياً على المستوى M فإنه تظهر حينئذ ثلاثة أوجه للمكعب في المستوى S ويسمى الشكل الناتج بالمسقط الأيزومتري.

ونتيجة لإدارة المكعب وإمالته بهذه الطريقة فإن مساقط أحرفه تظهر في المستوى S أقل من أطوالها الحقيقية بنسبة 19% تقريباً. ولكن يلاحظ أن النسبة بين الأحرف الثلاثة تظل ثابتة بدون تغيير.

ويجب ملاحظة أن زوايا المكعب القائمة تظهر في المسقط الأيزومتري بزوايا مقدارها إما 120° أو 60° وتسمى المحاور OZ, OY, OX بالمحاور الأيزومترية (Isometric Axes) وتسمى الخطوط الموازية لها أو التي تنطبق عليها بالخطوط الأيزومترية (Isometric lines).

وقد اتفق على أن يرسم المسقط الأيزومتري لجسم بحيث تؤخذ نفس أطواله الحقيقية إذا وقعت على الخطوط الأيزومترية ويسمى المنظور الناتج في هذه الحالة بالمنظور الهندسي ذو الوجهين المائلين 30° (Isometric).