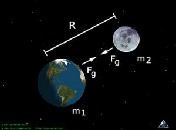
Newtonian mechanics of Gravitational energy – مجلة الامه العربيه

Newtonian mechanics

According to classical mechanics, between two or more masses (or other forms of energy–momentum) a gravitational potential energy exists. Conservation of energy requires that this gravitational field energy is always negative.^[2]
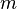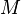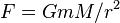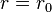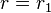Particularly, between any two point masses $m$ and $M$ (this works for the spherical bodies also), there always exists a gravitational force of $F = GmM/r^2$ where r is the distance between their centers. Increasing the distance from $r = r_0$ to $r = r_1$ reduces the force, but, since forces in Newton mechanics indicate how much potential energy is lost over space, 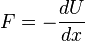$F = - {dU \over dx}$ , this separation requires $\int_{r_0}^{r_1}{mMG\over r^2} dr = \left . {mMG\over r} \right \vert _{r_1}^{r_0} = {mMG\over r_0} - {mMG \over r_1} = E$ of energy. Performing positive work equal to E units of energy, we can recede objects from r₀ to r₁ special units apart. By performing positive work equal to $E = {mMG / r_0}$ , the second term vanishes and objects are infinitely separated ( $r_1 = \infty$ ). Because gravitational force stops pulling objects together at that distance, $E = {mMG / r_0}$ is known as gravitational binding energy, which is infinite at $r_0 = 0$ since the gravitational force is infinite there^{[citation needed]}.