بحث رياضيات عن المثلثات – خصائص المثلث

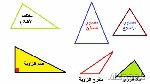
أوجه المثلث
يجب أن يكون مجموع أطوال أي من وجهي المثلث أكبر من طول الجانب الثالث، أو متساوية معه، وهذا يندرج تحت قاعدة عدم التساوي بين جوانب المثلث.
يمكن أن يساوي هذا الوجه طول الجانب الثالث فقط في حالة المثلث المنحل، وهو مثلث واحد برؤوس متداخلة، ولا يمكن أن يكون طوله أقل من طول الجانب الثالث، كما أنه من الممكن أن يتواجد مثلث بثلاثة أطوال جانبية موجبة، لكن فقط إذا كانت الأطوال الجانبية هذه غير متساوية.
زوايا المثلث
يوجد في المثلث ثلاث زوايا، ويكون مجموعهم 180 درجة، وتكون كل زاوية من زوايا المثلث قيمتها موجبة، على أن تكون قيمة الزاوية الواحدة أقل من 180 درجة، و إذا كان المثلث المنحل مسموحًا به؛ فيُسمح بزاوية 0 °.
يسمح هذا بتحديد مقياس الزاوية الثالثة لأي مثلث بالنظر إلى قياس الزاويتين المعروفة قيمتهما.
الزاوية الخارجية للمثلث هي الزاوية التي تكون مكملة للزاوية الداخلية، ويكون قياس الزاوية الخارجية للمثلث متساوٍ مع مجموع قياس الزاويتين الداخليتين غير المجاورتين له، وهذه هي نظرية الزاوية الخارجية؛ حيث أن مجموع مقاييس الزوايا الخارجية الثلاث لأي مثلث يبلغ 360 درجة.
التشابه والتطابق في المثلثات
يكون المثلثين متشابهين إذا كانت كل زاوية من المثلث لها نفس قياس الزاوية المقابلة في المثلث الآخر، كما أن الأطوال المقابلة للمثلثات المتشابهة لها أطوال متساوية في نفس النسبة، وهذه السمة تكفي أيضًا لإثبات التشابه.
بعض النظريات الأساسية حول المثلثات المتماثلة هي:
إذا كان هناك زوج من الزوايا الداخلية بمثلثين لهما نفس المقياس مع الآخر؛ فإن المثلثات تكون متشابهة.
إذا كان هناك زوج من الأضلاع المقابلة من مثلثين متماثلين في نفس النسبة مع زوج آخر من الأضلاع المقابلة، وزواياهم المتضمنة متساوية في القياس؛ فإن المثلثات في هذه الحالة تكون متشابهة، والزاوية الموجودة في أي جانب من جوانب المضلع هي الزاوية الداخلية بين هذين الجانبين.
إذا كانت الثلاثة أزواج من الجانبين المتماثلين لمثلثين كلها متماثلة في نفس النسبة؛ فإن المثلثات تكون متشابهة.